Comprendre l’informatique quantique – algorithmes et applications
Comprendre l’informatique quantique – algorithmes et applications
Par Olivier Ezratty, expert FrenchWeb

Maintenant que nous avons désossé un ordinateur quantique avec ses qubits, ses registres, ses portes et son frigo, voyons-donc comment on peut exploiter cette belle quincaillerie. L’ordinateur quantique utilise des algorithmes dits quantiques qui ont la particularité d’être bien plus efficaces que leurs équivalents conçus pour des ordinateurs traditionnels. Mais ces algorithmes ne sont pas très nombreux et leur performance relative aux algorithmes traditionnels pas toujours évidente à prouver. Elle est même parfois contestée.
Richard Feynman avait décrit l’idée de créer des simulateurs quantiques en 1982 dans Simulating Physics with Computers (22 pages). Son idée consistait à créer des dispositifs exploitant les effets de la mécanique quantique pour les simuler tandis que cette simulation serait quasiment impossible avec des ordinateurs traditionnels. Cela correspond aujourd’hui à l’un des usages des ordinateurs quantiques, comprenant notamment la simulation des interactions atomiques dans des structures inertes ou biologiques. On peut même faire la distinction entre simulateurs quantiques analogiques et simulateurs quantiques numériques, à base de qubits et de portes quantiques.
Des mathématiciens planchent depuis le milieu et la fin des années 1980 sur la création d’algorithmes adaptés aux simulateurs et ordinateurs quantiques, bien avant que l’on en ait vu l’ombre de la couleur. Les premiers algorithmes quantiques ont été publiés au début des années 1990 et les chercheurs en créent régulièrement de nouveaux depuis 25 ans. Le Quantum Algorithm Zoo en identifie une soixantaine dans la littérature scientifique ! C’est un nombre encore modeste au regard des algorithmes non quantiques qui se comptent en milliers.
Leur création est un travail de recherche parallèle avec la partie matérielle des ordinateurs quantiques. Ce n’est pas la première fois dans l’Histoire qu’il en est ainsi. L’emblématique Ada Lovelace planchait sur la création des premiers algorithmes et lignes de code devant tourner sur la machine de Charles Babbage, qui ne vit jamais le jour. Elle avait annoté en 1842/1843 une traduction de son cru d’un papier de l’Italien Luigi Federico Menabrea qui décrivait la machine de Babbage. Il fallut attendre 102 ans pour que les premiers ordinateurs voient le jour à la fin de la seconde guerre mondiale ! Cela rappelle dans un autre domaine les dessins d’hélicoptères de Léonard de Vinci qui datent de 1487-1490. Un premier hélicoptère propulsé par l’énergie humaine et créé par l’Université de Toronto a volé en 2013, AeroVelo (vidéo) suivi d’un autre spécimen assez voisin issu de l’Université de Maryland qui vient tout juste de voler en 2018 (vidéo) ! Donc, avec plus de cinq siècles de décalage ! Cette même Université de Maryland est d’ailleurs l’une des plus en pointe dans le monde dans les ordinateurs quantiques à base d’ions piégés ! Comme quoi !

Après-guerre, l’Histoire se répéta en partie pour nombre de travaux du vaste champ de l’intelligence artificielle, où les chercheurs planchaient également sur des algorithmes, notamment à base de réseaux de neurones, avant que les ordinateurs puissent les exécuter convenablement. L’essor du deep learning depuis 2012 est en partie lié à la puissance des machines et des GPU à même d’entraîner de tels réseaux de neurones. Le matériel a une fois encore rejoint les algorithmes qui étaient en avance sur leur temps.
Aujourd’hui, une bonne part des algorithmes quantiques qui sont inventés ne sont pas encore exécutables sur les ordinateurs quantiques disponibles ni même sur des simulateurs quantiques à base d’ordinateurs traditionnels. Les qubits sont disponibles dans un nombre bien trop faible pour qu’ils servent à quelque chose et surtout, qu’ils soient plus performants que ordinateurs traditionnels. Les supercalculateurs émulent difficilement plus de 50 qubits.
Comme dans le passé de l’Histoire de l’informatique, nous en sommes dans le quantique à naviguer dans les couches basses du logiciel. Un peu comme pour les programmeurs en langage machine ou en assembleur d’il y a 30 à 50 ans. Les algorithmes quantiques sont les couches les plus basses des solutions logicielles qui restent à inventer puis à assembler. Les algorithmes quantiques exploitent les portes quantiques que nous avons vues dans la partie précédente.
La création d’algorithmes quantiques requiert une capacité d’abstraction sans commune mesure avec celle des algorithmes et programmes traditionnels. Une nouvelle génération de mathématiciens et développeurs capables de raisonner en mode quantique devra se développer au gré de la maturation des ordinateurs quantiques. Ils devront être capables de conceptualiser des algorithmes qui ne sont pas faciles à se représenter physiquement. Qui plus est, ces algorithmes devront aussi, c’est la moindre des choses, être bien plus efficaces que leurs équivalents pour ordinateurs traditionnels ou supercalculateurs.
L’ambiguïté de la suprématie quantique
Avant de rentrer dans le détail des algorithmes quantiques, il nous faut expliquer la signification de la notion de “suprématie quantique” qui commence à fleurir dans la communication de certains acteurs tels que Google. C’est un terme un peu galvaudé dont vous entendrez parler dans diverses annonces tonitruantes à venir.
Voir par exemple New twists in the road to quantum supremacy et Google’s new chip is a stepping stone to quantum computing supremacy publiés dans la sérieuse MIT Technology Review en 2017. L’appellation a été inventée en 2011 par l’Américain John Preskill dans sa communication au Congrès de Solvay de cette année-là, décrite dans Quantum Computing and the Entanglement Frontier.
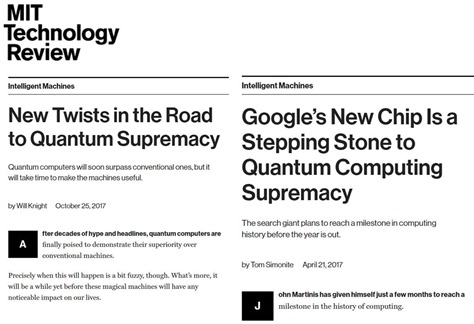
Une “suprématie quantique” est atteinte lorsqu’un algorithme traitant un problème donné n’est exécutable que sur un ordinateur quantique, ce problème ne pouvant pas être résolu même sur le plus puissant des supercalculateurs. De nombreux spécialistes affirment que le seuil de 50 qubits de qualité pur porc – avec un faible taux d’erreurs et un long temps de décohérence – constituera une étape clé de l’atteinte de cette suprématie quantique.
Mais cette appellation n’est pas absolue. Elle ne signifiera pas qu’un ordinateur quantique donné est suprêmement plus puissant que tous les supercalculateurs du moment. C’est une appellation qui devra être utilisée au cas par cas avec des couples d’algorithmes quantiques et d’ordinateurs quantiques, et avec des tests réalisés sérieusement avec le meilleur possible des algorithmes adaptés aux supercalculateurs sachant que celui-ci est aussi mouvant.
Certains benchmarks de D-Wave et Google réalisés en 2015 et montrant la supériorité de la solution quantique (dite adiabatique ou à recuit quantique) ont été ensuite contredits par la création d’algorithmes optimisés pour des supercalculateurs. Bref, cette suprématie quantique naviguera dans un premier temps dans des sables mouvants.

Elle interviendra certainement d’ici quelques années pour quelques algorithmes qui ne peuvent avoir d’équivalents optimisés pour les supercalculateurs. Voir à ce sujet Quantum Algorithms Struggle Against Old Foe: Clever Computers de Ariel Bleicher (février 2018) qui rappelle à juste titre que les supercalculateurs et ceux qui les exploitent n’ont pas dit leur dernier mot et cherchent aussi à améliorer leurs propres algorithmes. A long terme, le quantique supplantera certainement les supercalculateurs pour un grand nombre d’algorithmes.
Il semblerait sinon que les limitations des supercalculateurs pour simuler des algorithmes quantiques relèvent plus de leur mémoire vive que de leur capacité de traitement. Il faudrait 10 Po de mémoire pour simuler 48 qubits. Quand on arrive à 50 qubits, on dépasse la capacité mémoire des supercalculateurs d’aujourd’hui. Si on passe à 96 qubits, la mémoire nécessaire pour simuler l’ensemble sur supercalculateur est multipliée par 2 puissance 48. Bref, la loi de Moore de la mémoire ne peut pas suivre le rythme d’une augmentation linéaire du nombre de qubits alignés dans un ordinateur quantique.
Il faudra se méfier des annonces des IBM et autres Google lorsqu’ils prétendront avoir atteint cette suprématie quantique. Quand Google communiquait en mars 2018 sur la création d’un ordinateur quantique de 72 qubits, donc bien au-delà de 50 qubits, il se gardait bien de préciser le temps de cohérence de l’ensemble ainsi que du niveau du bruit généré, sans compter le fait qu’il n’avait pas encore été benchmarké avec un algorithme donné. Sans ces informations, une annonce d’ordinateur quantique reste du vent !
Il faut donc attendre d’avoir des éléments d’informations complets pour juger, comme l’indiquent fort bien Cristian et Elena Calude de l’Université d’Auckland en Nouvelle Zélande dans The road to quantum computing suppremacy publié fin 2017. Ils arguent aussi du fait que l’on compare une limite haute de performance, celle d’un ordinateur quantique précis, à une limite basse qui est la meilleure performance dans la résolution du même problème dans un supercalculateur. Or, il est plus facile de démontrer qu’un truc existe que son inexistence.
Une suprématie quantique est donc un comparable entre l’existence d’une performance quantique et la supposition de la non existence d’une performance équivalente dans le non quantique. Les auteurs rappellent aussi un critère qui manque parfois à l’analyse : il vaudrait mieux que l’algorithme testé serve à quelque chose ! Ce qui n’est pas toujours évident avec les algorithmes quantiques comme nous le verrons plus loin.
Usages des applications quantiques
Avant de rentrer dans le lard des algorithmes quantiques, faisons un détour de leur utilité pratique connue à ce jour.
Je les ai organisés ci-dessous en trois niveaux verticaux : les fonctions de base, les algorithmes puis les applications concrètes. Tout ceci relève encore largement de la prospective car nombre de ces solutions demanderont des puissances en termes de nombre et de qualité de qubits qui ne seront pas disponibles avant plusieurs années voire décennies.
Dans un ordre vaguement chronologique, nous aurons tout d’abord des applications d’algorithmes de recherche et d’optimisation basés sur les équations linéaires en général sachant que tous les algorithmes quantiques reposent sur des équations linéaires. On peut y caser les solutions de résolution de problèmes complexes, comme la détermination du parcours optimal d’un commercial, un sujet bien connu. Sa variante est la solution d’optimisation du trafic individuel de nombreux véhicules dans une ville en tenant compte de l’ensemble des trajets planifiés pour chacun d’entre eux.
Cette catégorie de solutions comprend aussi l’accélération de l’entraînement des réseaux de neurones du deep learning. L’avantage par rapport aux techniques existantes s’appuyant sur des processeurs neuromorphiques n’est pas encore évidente et démontrée. Qui plus est, la faisabilité de ces réseaux de neurones est établie sur architectures traditionnelles, à base de GPUs comme ceux de Nvidia ou de TPU (Tensor Processing Units) comme ceux de Google, sans compter les processeurs à base de memristors qui sont encore au stade du laboratoire.
En second lieu, dans le vaste champ de la simulation quantique, nous aurons d’abord des applications dans la chimie et la physique des matériaux pour simuler les interactions entre atomes dans molécules et structures cristallines, qui dépendent elles-mêmes des lois de la mécanique quantique. Cela servira si tout va bien à inventer de nouvelles solutions comme des batteries plus efficaces, chargeables plus rapidement et avec une plus grande densité énergétique, des procédés chimiques de captation du carbone ou de fixation de l’azote, ainsi que la création de matériaux supraconducteurs à température ambiante. Ce sont des hypothèses non encore validées à savoir que les algorithmes quantiques complétés d’ordinateurs quantiques bien dimensionnés avec des centaines de qubits logiques seront à même de permettre aux chercheurs d’avancer dans ces domaines-là.
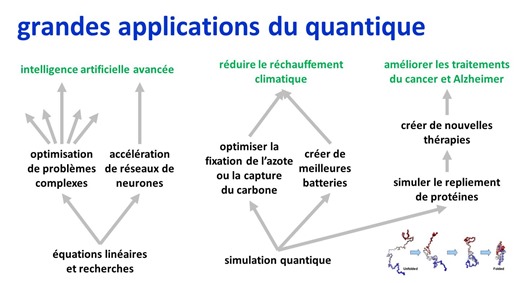
En dernier lieu et avec des quantités de qubits bien plus importantes, donc à plus lointaine échéance, la simulation quantique pourra éventuellement passer à la simulation de molécules biologiques. Cela commencera avec celle de peptides, puis de polypeptides, et enfin, de protéines et d’enzymes. Les molécules biologiques ont la particularité d’être très complexes, avec des structures pouvant atteindre des dizaines de milliers d’atomes. Le top du top serait la capacité à simuler l’assemblage puis le fonctionnement d’un ribosome, qui fait plus de 100 000 atomes. C’est la structure moléculaire la plus magique du vivant, celle qui assemble les acides aminés pour construire les protéines à partir du code de l’ARN messager issu de la transposition de l’ADN des gênes. Suivrait alors la simulation du fonctionnement d’une cellule entière. Mais là, on est à la frontière de la science-fiction, même en étant très optimiste sur l’informatique quantique !
Mon schéma est une version simplifiée d’un équivalent trouvé dans un rapport du Gartner Group de fin 2017, ci-dessous.
Principes de base
Comme nous l’avons vu dans la partie précédente qui décrit la structure d’un ordinateur quantique, un algorithme quantique va intégrer à la fois la partie initialisation des données puis celle des calculs et enfin de la mesure du résultat. Elle s’appliquera à un registre de n qubits qui sont physiquement initialisés à zéro, puis modifiés par des portes quantiques.
Le résultat correspond à la mesure de l’état de ces mêmes qubits à la fin de l’exécution de l’algorithme. Si le résultat recherché est purement binaire (0 ou 1 par qubits), le cycle ne sera exécuté qu’une seule fois. Si le résultat est une probabilité de 0 et de 1 pour chaque qubits, alors, il faudra répéter de nombreuses fois le cycle initialisation-algorithme-mesure et faire une moyenne des 0 et des 1 obtenu pour chaque qubit et obtenir un nombre flottant compris entre 0 et 1.
L’algorithme doit être compatible avec les caractéristiques de l’ordinateur quantique. Les principales sont le temps de cohérence et la durée d’exécution des portes quantiques. Le nombre de portes quantiques à exécuter devra permettre d’exécuter l’algorithme dans un temps inférieur au temps de cohérence au bout duquel les qubits perdront leur état de superposition. Cette vérification est généralement réalisée par les compilateurs de code quantique. Elle devra tenir compte des codes de correction d’erreurs qui sont souvent mis en œuvre sous la forme de sous algorithmes préfabriqués intégrés dans l’algorithme “métier” créé par le développeur.
Il en va de même des portes quantiques utilisées dans les outils de développement. Certaines portes quantiques, notamment s’appliquant sur deux ou trois qubits, sont utilisées par les développeurs mais seront converties par le compilateur en un jeu de portes quantiques universelles supportées par l’ordinateur quantique. Cela va aussi multiplier le nombre de portes quantiques par rapport à l’algorithme initial. Dans la pratique, l’ordinateur va donc exécuter un nombre de portes quantiques bien plus grand que l’algorithme conçu par le développeur.
L’une des considérations importantes de la création d’algorithmes quantiques est de s’assurer qu’ils sont plus efficaces que leurs équivalents optimisés pour des ordinateurs ou supercalculateurs traditionnels. Des théories permettent de vérifier cela pour évaluer la montée en puissance exponentielle, polynomiale, quadratique ou logarithmique du temps de calcul en fonction de la taille du problème à réaliser, ou une combinaison des quatre. Mais rien ne remplace l’expérience !
Les grandes classes d’algorithmes quantiques
Les algorithmes quantiques sont des applications pratiques de l’algèbre linéaire, cette branche des mathématiques qui gère des espaces vectoriels et des transformations linéaires à base de matrices. Elles sont appliquées dans des espaces à deux dimensions, les vecteurs qui définissent les états de qubits. Leur manipulation s’appuie sur des calculs matriciels qui permettent de modifier l’état des qubits sans en lire le contenu. Leur lecture n’intervient qu’à la fin des calculs. Cela rend difficile la programmation conditionnelle, du genre : faire tel calcul si tel résultat intermédiaire a telle valeur ou vérifie telle condition. Mais les portes quantiques conditionnelles (CNOT & co) permettent d’émuler ce genre de comportement dans un algorithme quantique.
A ce jour, quatre principales catégories d’algorithmes quantiques sont disponibles et que nous détaillerons plus loin :
- Les algorithmes de recherches basés sur ceux de Deutsch-Jozsa, Simon et de Grover.
- Les algorithmes basés sur les transformées de Fourier quantiques (QFT), comme celui de Shor qui sert à la factorisation de nombres entiers qui a déclenché un phénomène de pompiers-pyromanes, les pyromanes étant ceux qui veulent créer des ordinateurs quantiques capables de casser les clés de sécurité publiques de type RSA et les pompiers étant ceux qui cherchent à protéger les communications numérique avec des algorithmes résistant à la factorisation rapide de nombre entiers.
- Les algorithmes qui cherchent un point d’équilibre d’un système complexe comme dans l’entraînement de réseaux de neurones, la recherche de chemin optimal dans des réseaux ou l’optimisation de processus.
- Les algorithmes de simulation de mécanismes quantiques qui servent notamment à simuler les interactions entre atomes dans des structures moléculaires diverses, inorganiques et organiques.
La roadmap ci-dessous illustre le rythme de création de ces nouveaux algorithmes sur les trois dernières décennies. Et l’histoire ne fait que commencer parce que la dynamique d’innovation exponentielle du thème est pour l’instant limitée par l’imagination humaine et surtout, par les capacités d’expérimentation.
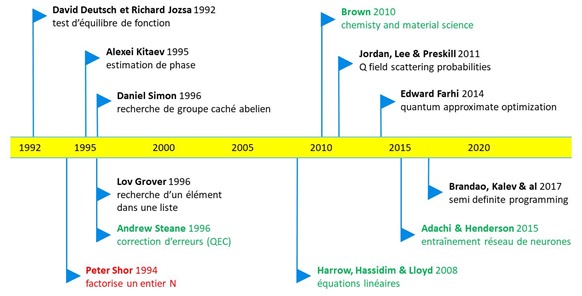
Voici quelques sources d’information pour creuser la question : Quantum Computing Applications d’Ashley Montanaro de l’Université de Bristol, 2013 (69 slides), Introduction à l’information quantique de Yves Leroyer et Géraud Sénizergues de l’ENSEIRB-MATMECA, 2016-2017 (110 pages), un cours récent intéressant sur la partie algorithmique, An Introduction to Quantum Computing de Phillip Kaye, Raymond Laflamme et Michele Mosca, Oxford, 2017 (284 pages), Lecture Notes on Quantum Algorithms de Andrew M. Childs, University of Maryland, 2017 (174 pages), Quantum Computation and Quantum Information de Nielsen et Chuang, 2010 (698 pages) et A Course in Quantum Computing for the Community College de Michael Locef, 2016 (742 pages) qui pose de manière très détaillée les fondements mathématiques du calcul et des algorithmes quantiques et nécessite plusieurs semaines pour être parcouru et compris.
En complément, voici quelques vidéos sur ce même sujet : Quantum Algorithms d’Andrew Childs en 2011 (2h31), Language, Compiler, and Optimization Issues in Quantum Computing de Margaret Martonosi, 2015 (39 minutes et slides) et What Will We Do With Quantum Computing? de Aram Harrow, MIT, 2018 (32 minutes).
Les algorithmes quantiques sont classifiables et explicables à haut niveau, mais leur compréhension détaillée n’est pas une partie de plaisir. Il faut soit avoir une capacité de vision conceptuelle assez développée, soit une maitrise des mathématiques poussée, et idéalement les deux à la fois. Dans ce qui suit, je vais donc vous décrire quelques algorithmes mais en reconnaissant que je n’ai pas véritablement tout compris de leur fonctionnement dans les qubits et opérations de portes quantiques appliquées dessus. Le quantique est ainsi fait en général : on n’a jamais tout compris ! Décrire cela est donc un véritable exercice d’humilité intellectuelle.
Algorithmes de recherche
L’un des premiers algorithmes quantiques inventés est celui de David Deutsch, avec sa déclinaison dite de Deutsch-Jozsa, coinventée avec Richard Jozsa et qui date de 1992. Cet algorithme permet de caractériser la fonction d’une “boite noire” que l’on appelle un “oracle” dont on sait à l’avance qu’elle va retourner pour toutes ses entrées, soit toujours la même valeur, 0 ou 1, soit les valeurs 0 et 1 à parts égales. L’algorithme permet donc de savoir si la fonction f() est équilibrée ou pas. Elle est appliquée à un ensemble de qubits n.
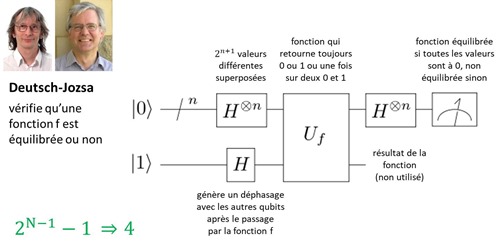
Les qubits en entrée sont tous initialisés à 0 sauf un qui l’est à 1 puis ils sont chacun mis en superposition entre 0 et 1 via des portes de Hadamard. Les qubits ont donc simultanément toutes les valeurs possible avec 2 puissance n+1 combinaisons de valeurs. Il est facile de comprendre pourquoi cet algorithme quantique est bien plus efficace que sa version traditionnelle : en calcul traditionnel, il faudrait scanner plus de la moitié des valeurs possibles en entrée de manière séquentielle alors que dans la version quantique, elles sont toutes analysées en même temps. Le résultat est donc obtenu avec quelques séries de portes quantiques, presque instantanément, et il est parfaitement déterministe.
Ces qubits en superposition traversent la boite noire qui contient un ensemble de portes avec une fonction à évaluer. On mesure alors en sortie le résultat pour voir si la fonction est équilibrée ou pas grâce à d’autres portes de Hadamard. L’initialisation du dernier qubit à 1 sert à générer une interférence avec les autres qubits qui va impacter les valeurs sortant des portes H après le passage par l’oracle. La fonction f est constante si la totalité des mesures donne 0 et déséquilibrée si au moins d’un des qubits en sortie retourne 1. Pour savoir comment cela fonctionne dans le détail, vous pouvez voir les formules mathématiques associées ainsi que la présentation Deutsch-Jozsa Algorithm de Eisuke Abe, 2005 (29 slides). Mais ce n’est pas des plus évident ! Les explications données sont toujours incomplètes pour bien comprendre ces algorithmes. Elles n’indiquent pas bien où se retrouve le bit de sortie de la fonction de l’oracle qui est soit de 0 soit de 1.
L’intérêt pratique ? C’est un exemple d’algorithme ultra puissant qui n’a aucune utilité pratique connue à ce jour. On est bien avancés ! Qui plus est, il existe des algorithmes probabilistes classiques très efficaces qui effacent une bonne part du gain de puissance quantique de l’algorithme de Deutsch-Jozsa. C’est le cas en particulier de l’algorithme de recherche de Monte Carlo qui évalue la fonction d’oracle sur un nombre limité d’entrées choisies aléatoirement. La probabilité d’erreurs est dépendante du nombre d’évaluations et décroit très rapidement. Voir à ce sujet le document Modèles de Calcul Quantique (30 pages).
Alors, le quantique ne sert donc à rien ? Non, bien sûr. D’autres algorithmes moins performants mais bien plus utiles ont vu le jour depuis ce patient zéro de l’algorithmie quantique !
L’algorithme de Simon est une variante plus complexe de celui de Deutsch-Jozsa. Il consiste à trouves les combinaisons de valeurs qui vérifient une condition imposée par la fonction “boite noire”. Le gain de performance est très intéressant et cette fois-ci, les applications existent, notamment pour résoudre des problèmes de parcours dans des graphes. Le gain de performance est typique de ce que le quantique apporte : on passe d’un calcul classique qui est de temps exponentiel (2 puissance n/2) à un temps linéaire en N.
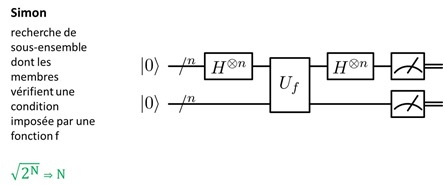
L’autre algorithme le plus connu de cette catégorie est celui de Grover, créé en 1996. Il permet de réaliser une recherche quantique rapide dans une base de données. Un peu comme l’algorithme de Deutsch-Jorza, il permet de scanner une liste d’éléments pour trouver ceux qui vérifient un critère. Il utilise aussi la superposition d’états de qubits pour accélérer le traitement par rapport à une recherche séquentielle traditionnelle dans une base non triée et non indexée. L’amélioration de performance est significative par rapport à une base non triée, à ceci près que dans la vraie vie, on utilise généralement des bases indexées !
L’algorithme de Grover utilise aussi une fonction “oracle” ou “boite noire” qui va indiquer si un ensemble de qubits en entrée vérifie un critère de recherche ou non, comme pour vérifier qu’un numéro de téléphone donné a été trouvé dans une liste de numéros de téléphone. Dans un tel cas, la fonction compare le numéro de téléphone recherché et celui qui lui est soumis pour répondre 1 si ils sont identiques et 0 sinon. La boite noire étant quantique, elle va évaluer cette fonction pour 2 puissance N registres de qubits en même temps. Elle sortira donc un 1 une fois et des 0 autrement. La question étant de savoir si un 1 est sorti une fois et à quelle entrée il correspond. Pour ce faire, là aussi avec des portes de Hadamard, l’algorithme va amplifier graduellement la combinaison de qubits du résultat à une valeur 1 et faire converger les autres combinaisons de qubits vers 0. Il sera alors possible de mesurer le résultat et on obtiendra la combinaison de qubits avec la valeur recherchée.

Le temps de calcul est proportionnel à la racine carrée de la taille de la base et l’espace de stockage nécessaire est proportionnel au logarithme de la taille de la base. Un algorithme classique a un temps de calcul proportionnel à la taille de la base. Passer d’un temps N à sqrt(N) est donc un gain intéressant, mais il ne transformera pas un problème de taille exponentielle en problème de taille polynomial (2 puissance N vers N puissance M).
Par contre, cet algorithme peut ensuite être exploité pour être intégré dans d’autres algorithmes comme ceux qui permettent de découvrir le chemin optimal dans un graphe ou le nombre minimal ou maximal d’une série de N nombres.
Notons cependant que l’algorithme de recherche de Grover nécessite l’emploi d’une mémoire quantique (QRAM) qui n’est pas encore au point ! C’est notamment documenté dans Quantum algorithms for linear algebra de Anupam Prakash, 2015 (92 slides).
Ces différents algorithmes de recherche sont déclinés en diverses variantes et sont exploités en pièces détachées dans d’autres algorithmes quantiques.
Transformées de Fourier quantiques et usages associés
Les transformées de Fourier classiques permettent d’identifier les fréquences qui composent un signal. En théorie du signal, cela permet d’identifier les composantes de base d’un son en le décomposant en fréquences. En astrophysique, on détermine la composition atomique des étoiles par une décomposition du spectre lumineux, mais celle-ci est opérée par un prisme optique et pas par transformée de Fourier. Il en va de même pour les capteurs en proche infrarouge de type Scio qui déterminent la composition des aliments. Un prisme et le principe de la diffraction permettent donc de réaliser optiquement une transformée de Fourier.
La transformée de Fourier quantique est utilisée dans divers autres algorithmes et en particulier dans celui de Shor qui sert à factoriser des nombres entiers. Elle n’est pas une transformée parfaite qui réalise une décomposition complète en fréquences d’un signal. Elle sert à identifier la fréquence d’amplitude la plus forte d’un signal donné. Elle ne peut pas servir à du traitement fin du signal comme on le fait dans des DSP (Digital Signal Processors) traditionnels.
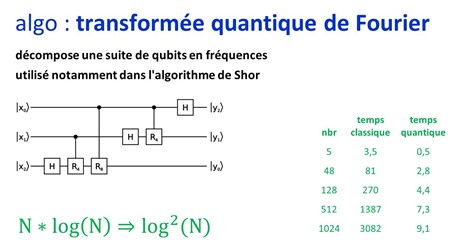
Le gain de vitesse généré ? Le temps de calcul passe de N*log(N) pour les meilleures transformées de Fourier simples à log2(N) pour la QFT. On passe donc d’un ordre de grandeur linéaire à un ordre de grandeur logarithmique. C’est un gain appréciable mais pas très impressionnant.
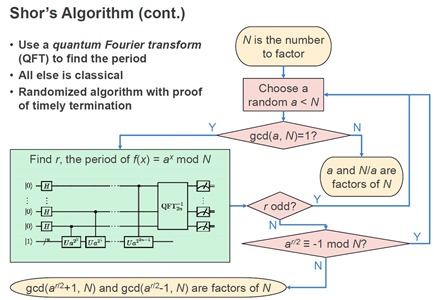
La factorisation de Shor permet permet de décomposer des entiers en nombres premiers bien plus rapidement qu’avec un ordinateur traditionnel. Elle utilise une QFT vue précédemment. Je vous passe les détails du fonctionnement de l’algorithme qui est décrit dans le schéma ci-dessous (source) et dans cette explication assez claire vue dans une vidéo de PBS.
L’une des premières mises en œuvre de l’algorithme de Shor eu lieu en 2001 chez IBM avec un ordinateur quantique expérimental de 7 qubits, pour factoriser le nombre 15. Depuis, on est juste passé à un nombre à 5 chiffres, 56153, comme documenté dans Quantum factorization of 56153 with only 4 qubits, 2014 (6 pages), mais avec un autre algorithme de factorisation que celui de Shor. C’est en fait un algorithme d’optimisation qui fonctionnait sur ordinateur à recuit quantique du Canadien D-Wave ! Le record à ce jour atteint en 2016 serait la factorisation de 200 099 avec 897 qubits sur D-Wave mais avec un autre algorithme que celui de Peter Shor. Comme quoi il ne faut pas jeter le bébé D-Wave avec l’eau du bain du quantique universel !
Il faut surtout retenir que l’algorithme de Shor permet en théorie de casser les clés publiques de la cryptographie RSA qui est couramment utilisée dans la sécurité sur Internet. Les clés publiques fonctionnent en envoyant un très long nombre entier à un destinataire qui possède déjà son diviseur. Il lui suffit de diviser le grand nombre envoyé par son diviseur pour récupérer l’autre diviseur et décoder le message ainsi chiffré. Celui qui ne possède pas le diviseur ne peut pas exploiter la clé complète sauf à disposer d’une énorme puissance de calcul traditionnelle pour trouver ses diviseurs. Jusqu’à présent, seuls les supercalculateurs de la NSA pouvaient casser les clés de taille raisonnable comprises aux alentours de 256 à 400 bits. Mais à 512, 1024 bits et au-delà, la tâche est inaccessible en un temps raisonnable pour ces supercalculateurs.
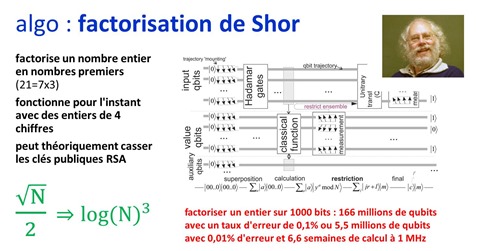
En théorie, cela deviendrait accessible à des ordinateurs quantiques. Mais pour casser une clé publique RSA de 1024 bits, il faudra encore patienter car cela nécessite de créer des ordinateurs quantiques avec un très grand nombre de qubits fonctionnant en cohérence. On en est très très loin. A noter que l’algorithme de Shor permet aussi de casser la cryptographie utilisant des courbes elliptiques, qui concurrencent la cryptographie RSA. Au passage, une bonne part de la cryptographie utilisée dans le protocole du Bitcoin passerait également à la moulinette Shor, mais pas des blockchains d’Ethereum.
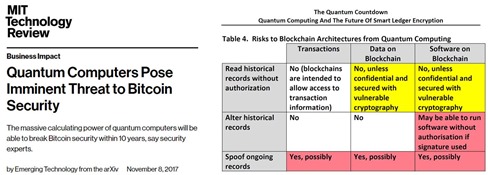
En tout cas, l’algorithme de Shor terrorise les spécialistes de la sécurité depuis une bonne dizaine d’années. Cela explique l’intérêt pour l’exploitation de clés quantiques, censées être inviolables car leur interception peut être détectée par son récipiendaire légitime, ainsi que de la “post quantum cryptographie” consistant à faire évoluer les algorithmes et méthodes de cryptographie pour les rendre (théoriquement) inviolables par des ordinateurs quantiques utilisant l’algorithme de Shor. Les deux méthodes étant probablement combinables. Nous aurons l’occasion de traiter de cela plus tard.
Algorithmes de machine learning et de deep learning
Quelques algorithmes d’optimisation quantiques divers existent également. Ils peuvent permettre diverses optimisations combinatoires utiles dans divers métiers comme dans le marketing ou la finance.
L’un de ces algorithmes relève de l’entraînement de réseaux de neurones. Mais cela ne change pas les fonctionnalités accessibles, qui sont déjà exploitables. Cela ne jouera un rôle que le jour où on alignera des millions de qubits avec un faible niveau d’erreurs. Cela va d’ailleurs poser des problèmes d’explicabilité des algorithmes car on ne pourra pas facilement expliquer les résultats. La décomposition du processus d’entraînement et d’inférence de ces réseaux de neurones quantiques sera probablement différente par rapport à leur mise en œuvre dans des ordinateurs plus traditionnels.
Ces algorithmes quantiques de réseaux de neurones doivent contourner le fait que les fonctions d’activation des neurones sont généralement non linéaires, comme les sigmoïdes qui sont couramment utilisées alors que les portes quantiques appliquent toutes des transformations linéaires. L’astuce est expliquée dans Quantum Neuron: an elementary building block for machine learning on quantum computers, de Yudong Cao, Gian Giacomo Guerreschi et Alan Aspuru-Guzik en 2017 (30 pages).
Ces techniques seront concurrencées par les futurs processeurs neuromorphiques à base de memristors qui permettront de faire converger plus rapidement les réseaux par rétropropagation. C’est encore un domaine de recherche, opéré notamment par Julie Grollier du laboratoire du CNRS situé chez Thalès TRT à Palaiseau, et que j’ai pu rencontrer en mai 2018.
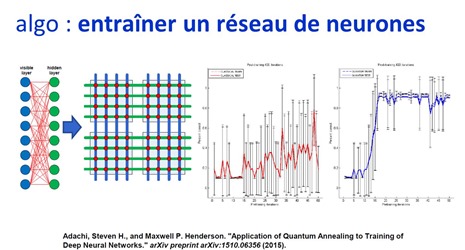
Voici quelques autres exemples d’algorithmes d’entraînement de machine learning provenant de D-Wave et exploitant leurs ordinateurs à recuit quantique.
Comme ils sont adaptés à la recherche d’un minimum énergétique de systèmes complexes, ils peuvent en effets servir à entrainer des réseaux de neurones, celui-ci correspondant à la recherche d’un niveau minimum d’erreur dans l’ajustement du poids des neurones.
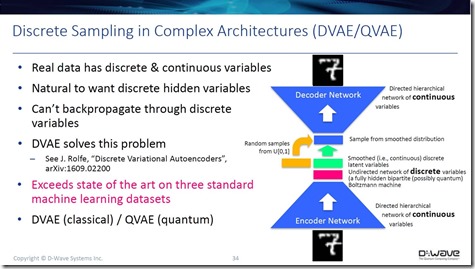
D-Wave fournit d’ailleurs les ressources de ses calculateurs quantiques en mode “cloud”.
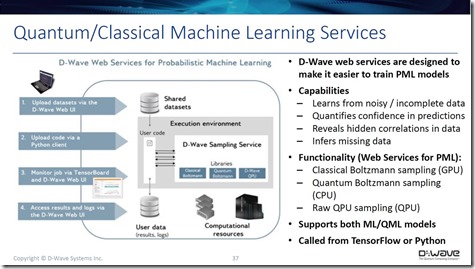
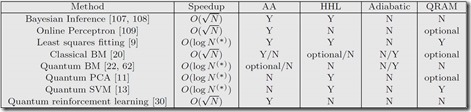
Dans Quantum Machine Learning, mai 2018, on trouve ce tableau qui positionne clairement les différentes accélérations quantiques associées à divers algorithmes utilisés dans le machine learning et le deep learning. Les accélérations en log(N) sont plus importantes que celles qui sont exprimées en racine carré de N. Ce document évoque de nombreux algorithmes quantiques de bas niveau qui sont très utiles au machine learning et au deep learning : le qBLAS (quantum basic linear algebra subroutines), la résolution d’équations linéaires, la descente de gradient pour la rétropropagation dans l’entraînement des réseaux de neurones, la PCA pour déterminer les variables clés d’un jeu de données (Principal Component Analysis, utilisée dans le machine learning traditionnel) et le SVM (support vector machine, une méthode traditionnelle de segmentation dans le machine learning). Le tout, avec une amélioration exponentielle de vitesse de traitement.
Il existe même des algorithmes quantiques de GAN (Generative Adversarial Networks), pour ces réseaux de neurones qui génèrent des contenus synthétiques à partir de contenus existants en vérifiant leur plausibilité via un réseau de neurones de reconnaissance. C’est bien documenté dans Quantum generative adversarial learningde Seth Lloyd et Christian Weedbrook, 2018 (5 pages).
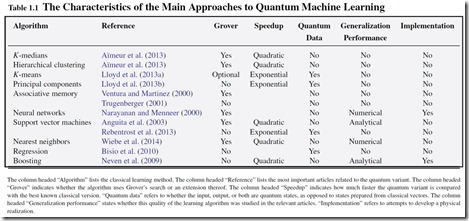
On retrouve cette liste d’algorithmes de machine learning en version quantique dans Quantum Machine Learning What Quantum Computing Means to Data Mining de Peter Wittek, 2014 (178 pages).
Côté sources d’information sur ce sujet, j’ai aussi parcouru Application of Quantum Annealing to Training of Deep Neural Networks. (2015), On the Challenges of Physical Implementations of RBMs, 2014, avec notamment Yoshua Bengio et Ian Goodfellow parmi les auteurs, illustrant l’intérêt des spécialistes de l’IA pour le quantique et Quantum Deep Learning, 2014, le tout étant extrait de Near-Term Applications of Quantum Annealing, 2016, Lockheed Martin (34 slides).

Bon, de là à utiliser ces algorithmes dans la robotique comme décrit dans The Rise of Quantum Robots de Daniel Manzano (avril 2018), il faudra patienter un peu ! Ce n’est plus de la technologie, c’est de la science-fiction.
Algorithmes de simulation quantique
Les algorithmes de simulation quantique servent à reproduire dans un ordinateur les phénomènes de la mécanique quantique qui gouvernement le comportement de quantums dans des ordinateurs traditionnels ou quantiques. Ils seront utilisables en particulier pour simuler l’interaction entre les atomes dans des molécules pour la création de nouveaux matériaux. Suivront la simulation des molécules de la biologie moléculaire, donc, de la chimie organique, allant progressivement des plus petites aux plus grandes des molécules : acide aminés, peptides, polypeptides, protéines et peut-être bien plus tard, de molécules ultra complexes comme les ribosomes qui fabriquent les protéines à partir des acides aminés. La constitution et le fonctionnement de ces grosses molécules font partie des plus grands mystères chimiques de la vie que l’Homme aimerait bien expliquer.
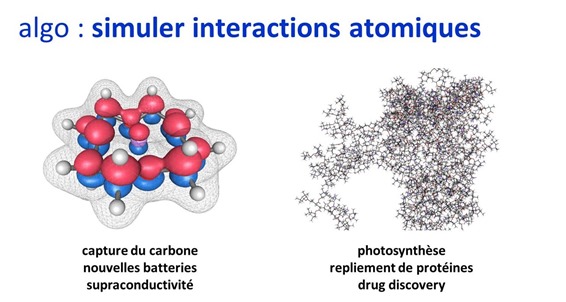
Bref, ces algorithmes ambitionnent de simuler les processus moléculaires qui interviennent dans la nature ou à créer de tels mécanismes artificiels qui n’existent pas encore dans la nature. Cela peut aussi servir à faire des simulations “macro” comme celle du fonctionnement de trous noirs ou d’étoiles à neutrons en astronomie.
Ces algorithmes s’exécuteront de manière la plus performante dans les ordinateurs quantiques universels à base de qubits. En attendant, on les exécute dans des ordinateurs adiabatiques comme ceux de D-Wave voire dans des ordinateur quantiques dits analogiques, sans architectures à base de registres de qubits. Comme ces algorithmes visent souvent à déterminer un niveau d’énergie minimum d’un système complexe, le système adiabatique à recuit simulé de D-Wave est assez adapté à la tâche pour des problèmes relativement simples.
A partir de 50 électrons dans une molécule, les ordinateurs classiques ne peuvent plus simuler leur dynamique, ce qui correspond à quelques atomes à peine. Pour les molécules simples, les applications relèvent de la physique des matériaux : capture du carbone ou de l’azote, nouvelles batteries, découverte de mécanismes supraconducteurs utilisables ensuite dans les scanners médicaux, idéalement fonctionnant à température ambiante.
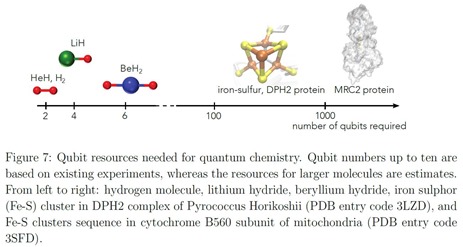
Ceci devrait être accessible avec des ordinateurs quantiques universels dotés de 50 à quelques centaines de qubits de qualité. Pour les simulations de biologie moléculaire, il faudra probablement attendre bien plus longtemps avant que cela soit possible et disposer d’ordinateur avec des milliers voir des centaines de milliers de qubits. Le schéma ci-dessous positionne de manière assez optimiste le nombre de qubits nécessaires pour simuler le fonctionnement une protéine des mitochondries, la MRC2. Il est issu de Quantum optimization using variational algorithms on near-term quantum devices, issu de chercheurs d’IBM en 2017 (30 pages).
Voici quelques exemples d’algorithmes de simulation quantique :
- Faster phase estimation de Svore, Hastings et Freedman, 2013 (14 pages) qui est utilisé dans les simulations quantiques de molécules.
- Solving strongly correlated electron models on a quantum computer de Wecker, Troyer, Hastings, Nayak et Clark, 2015 (27 pages), qui utilise les ordinateurs quantiques adiabatiques pour simuler la dynamique des semi-conducteurs.
- Simulated Quantum Computation of Molecular Energies de Wiebe, Wecker et Troyer, 2006 (21 pages) qui porte sur la détermination de l’état d’équilibre de molécules simples.
- Simulation of Electronic Structure Hamiltonians Using Quantum Computers de James Whitfield, Jacob Biamonte et Alan Aspuru-Guzik, 2010 (22 pages) qui porte aussi sur la simulation du fonctionnement de molécules simples.
- Un exemple de simulation de molécule d’hydrure de béryllium (3 atomes, BeH2) avec seulement 6 qubits par IBM en 2017 dans Tiny Quantum Computer Simulates Complex Molecules par Katherine Bourzac.
- La simulation de l’électrolyse de l’eau provoquée par de la lumière avec des usages évidents pour la production d’énergie stockable, notamment dans les piles à combustible (à base d’hydrogène). C’est l’un des très nombreux exemples issus de la présentation Enabling Scientific Discovery in Chemical Sciences on Quantum Computers, décembre 2017 (34 slides) par Ber De Jong de Berkeley.
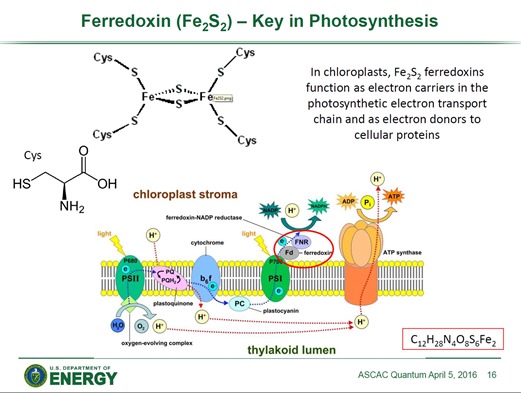
Dans Quantum Computation for Chemistry, 2009 (51 slides), on découvre que les caractéristiques des ordinateurs quantiques nécessaires pour simuler l’état de molécules organiques de complexité moyenne telle que le cholestérol, il faudrait 1500 qubits et surtout, pouvoir enquiller des milliards de portes quantiques, ce qui est actuellement impossible au vu des temps de cohérence bien trop courts des ordinateurs quantiques existants. Et on parle probablement d’un nombre de qubits logiques et pas physiques. Il faudrait donc probablement aligner des millions de qubits physiques pour pouvoir réaliser ce genre de simulation.
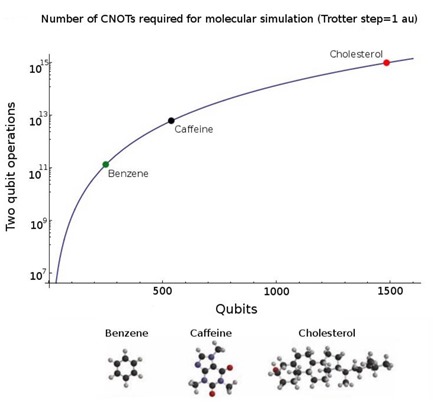
L’une des applications de la simulation quantique moléculaire est de mieux comprendre le fonctionnement de la photosynthèse pour éventuellement l’améliorer ou l’imiter, comme ci-dessous avec l’implication des différentes formes de ferrédoxine, des molécules relativement simples à base de fer et de souffre qui servent à transporter les électrons de l’effet photoélectrique mis en œuvre dans la photosynthèse dans les plantes. Les recherches algorithmiques sur la simulation de cette molécule ont fait passer en quelques années la durée de simulation théorique quantique de 24 milliards d’années à une heure !
Matthias Troyer explique comment cet algorithme a été optimisé dans What Can We Do with a Quantum Computer (41 slides). Dans le même domaine, la simulation de l’enzyme nitrogénase qui transforme l’azote en ammoniaque dans les cyanobactéries permettrait de produire des engrais avec beaucoup moins d’énergie que les processus habituels Haber-Bosch de production de l’ammoniaque qui sont très consommateurs d’énergie.

Il y présente les bénéfices d’autres forme d’optimisations, par simplification du modèle, pour la simulation de supraconducteurs.

S’il faudra être patient pour voir la couleur de nombre de ces simulations, cela n’empêche pas de nombreux chercheurs d’explorer des moyens de simuler le repliement de protéines, l’une des tâches de simulation de molécule organique les plus complexes. Voir par exemple Evolution, energy landscapes and the paradoxes of protein folding de Peter Wolynes, 2015 (13 pages).
Le top du top de la simulation moléculaire quantique arrivera probablement bien plus tardivement. Il s’agit de la simulation du repliement des protéines, une voie clé pour créer de nouvelles thérapies diverses, notamment pour traiter certaines pathologie neurodégénératives ou divers cancers. Différents algorithmes quantiques ont déjà été créés pour ce faire et notamment celui de Aspuru-Guzik de Harvard en 2012, qui a même été testé à petite échelle sur le premier ordinateur quantique adiabatique, le D-Wave One. Reste à évaluer les ordres de grandeur des ordinateurs quantiques nécessaires pour résoudre ces problèmes de chimie organique. Il n’est pas impossible qu’ils relèvent de l’impossible ou de l’extrême long-terme !
Pour en savoir plus, voir Quantum Information and Computation for Chemistry, 2016 (60 pages), qui inventorie très bien les divers travaux algorithmiques de simulation quantique de chimie organique.
Equations linéaires
Enfin, de nombreux autres algorithmes quantiques existent qui permettent de réaliser des opérations mathématiques complexes comme la résolution d’équations différentielles, l’inversion de matrices ou le traitement de divers problèmes d’algèbre linéaire. Ils sont ensuite utilisés… ailleurs ! L’algorithme le plus connu est le HHL qui reprend le nom de ses créateurs Harrow, Hassidim et Lloyd, créé en 2009 et qui qui permet de résoudre des équations linéaires, avec un gain de performance exponentiel.
Pour conclure, j’ai consolidé le petit schéma ci-dessous qui résume les gains de performance de quelques-uns des algorithmes déterministes que nous venons de voir. Les niveaux de complexité (exponentielle, polynomiale, linéaire, …) sont génériques. Les niveaux précis de complexité de chaque algorithme sont associés à ces classes de manière approximative. Ainsi, N*log(N) qui est la complexité d’une transformée de Fourier classique est linéaire car N grandit bien plus vite que log(N) et log(N) puissance 3 est une complexité de niveau logarithmique (pour l’algorithme de Shor et une QFT, Quantum Fourier Transform).
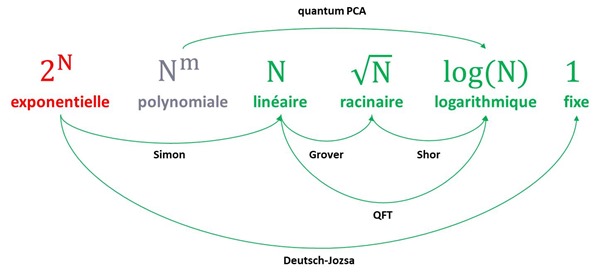
L’idéal en gains de performances est traverser plusieurs classes de complexité, et surtout, à partir d’un problème exponentiel. Dans la pratique, les principaux algorithmes sautent une à deux classes de complexité mais pas forcément à partir de la classe des problèmes exponentiels. Mais mon schéma est trompeur. N peut aussi croitre de manière exponentielle selon la taille d’un problème. L’exemple classique est celui de l’algorithme de Shor. Le point de départ est un N qui est en fait une taille de clé RSA qui elle-même est évaluée en puissance de 2. Une clé de 1024 bits fait 2 puissance 1024. Si on passe de 2 puissance 256 à 2 puissance 1024, la croissance de la taille de la clé est exponentielle. Et là, on obtient donc avec l’algorithme de Shor un gain de performance exponentiel en passant d’une racine carrée de 2 puissance 1024 à un log de 2 puissance 1024.
L’algorithme de Deutsch-Jozsa a la particularité de traverser tous les niveaux de complexité mais nous avons vu qu’il n’avait malheureusement pas d’application pratique connue. Il faut aussi intégrer le fait que la complexité de certains problèmes peut être contournée avec des approches probabilistes qui permettent aussi de réduire de un ou plusieurs étages le niveau de complexité de problèmes exponentiels. Bref, les algorithmes quantiques sont séduisants mais ils ne sont pas pour autant toujours la panacée.
_________________________
Dans la prochaine partie, nous étudierons justement la question des différents niveaux de complexité des problèmes qui peuvent être résolus par les ordinateurs classiques et quantiques et aussi ceux qui ne peuvent pas l’être par ces derniers. Cela remettra l’Homme dans sa posture classique : toujours à la recherche du savoir absolu, mais éternellement bloqué par de nouvelles barrières à surmonter.
L’expert:

Olivier Ezratty est consultant en nouvelles technologies et auteur d’Opinions Libres, un blog sur les médias numériques (TV numérique, cinéma numérique, photo numérique), et sur l’entrepreneuriat (innovation, marketing, politiques publiques…). Olivier est expert pour FrenchWeb.

Trois profils ont été retenus par Orange pour succéder à Stéphane Richard, condamné en novembre dans l’affaire Tapie/Crédit Lyonnais, au poste de directeur général, a-t-on appris vendredi auprès de sources proches du dossier, confirmant une information du quotidien Libération.
Ramon Fernandez, directeur général délégué d’Orange, Christel Heydemann, présidente de Schneider Electric France et membre du conseil d’administration d’Orange, et Frank Boulben, responsable des ventes de l’opérateur américain Verizon, ont été retenus par le comité de sélection interne du groupe. A la tête de l’opérateur historique depuis 2011, Stéphane Richard, qui cumule les postes de président et directeur général, doit quitter ses fonctions au 31 janvier au plus tard, alors que son mandat courait jusqu’à mi-2022.
Cette période de quelques semaines doit laisser le temps de sélectionner les candidats pour prendre son relais et acter la mise en place de la nouvelle gouvernance de l’entreprise, sur laquelle l’Etat, premier actionnaire avec plus de 20% du capital, a son mot à dire. Un scénario étudié depuis plusieurs mois est quasi certain: la dissociation des fonctions de président et directeur général pour le prochain mandat. Plusieurs groupes dont l’Etat est actionnaire ont mis en place une telle gouvernance, comme Renault, après le départ de Carlos Ghosn, ou Engie, où Gérard Mestrallet est passé en 2016 de PDG à président non exécutif.
« D’autres profils » recherchés
Selon plusieurs médias, cette liste de trois candidats n’emballerait toutefois ni Bercy, ni l’Elysée qui pourraient demander à chercher « d’autres profils » et repousser la date butoir du 31 janvier. Ce qui permettrait à Stéphane Richard de rester en poste quelques semaines de plus. Contacté par l’AFP, Bercy n’a pas fait de commentaires sur ce sujet.
Présent dans 26 pays dans le monde, Orange est un mastodonte qui emploie plus 140 000 salariés, dont plus de 80 000 en France, et a réalisé un chiffre d’affaires de 42,27 milliards d’euros en 2020. Stéphane Richard, à l’époque directeur de cabinet de la ministre de l’Economie Christine Lagarde, a été reconnu coupable en novembre de complicité de détournement de biens publics dans l’affaire de l’arbitrage controversé rendu en 2008 entre l’homme d’affaires Bernard Tapie, depuis décédé, et le Crédit Lyonnais.
[Serie E] 254 millions d’euros de plus pour la solution de paie en ligne Payfit
Avec notre partenaire Junto, spécialiste de la performance média, découvrez l'actualité des levées de fonds

Fondée en 2016, la startup spécialisée dans la gestion de la paie en ligne pour les PME vient de finaliser une 6ème levée de fonds d’un montant de 254 millions d’euros, 9 mois après avoir enregistré un tour de table de 90 millions d’euros.
Payfit profite du fort dynamisme du capital risque mondial et le déploiement en europe de nombreux fonds étrangers qui accélèrent leurs prises de participations notamment sur les startups en phase de croissance. Une opportunité que n’a pas manqué de saisir les fondateurs de la société en accueillant un nouvel actionnaire avec General Atlantic qui mène ce tour et fait s’envoler la valorisation de la société à plus de 1,82 milliard d’euros.
La société qui a levée 433 millions d’euros depuis sa création, compte parmi ses actionnaires Eurazeo, Bpifrance via son fonds Large Venture, Accel, Frst, Xavier Niel, Oleg Tscheltzoff, ou encore Thibaud Elzière
PayFit propose aux TPE et PME d’automatiser la gestion de la paie et la gestion administrative de leur personnel (déclarations sociales, congés, absences, notes de frais, suivi du temps de travail, intégration des nouveaux employés).
Avant de nouveaux développements internationaux, la scale up ambitionne de renforcer ses parts de marché en France, en Espagne, en Allemagne, au Royaume-Uni et en Italie.
La stratégie de l’entreprise est privilégier le renforcement de son offre de services et d’augmenter son chiffre d’affaires sur sa base client actuelle de 6000 clients TPE et PME. Parmi les nouveaux outils Payfit devrait proposer prochainement la gestion des entretiens annuels, ainsi que celle des notes de frais, ou encore un service d’avance sur salaire.
Pour assurer son développement Payfit doit recruter rapidement plus de 400 nouveaux collaborateurs, qui vont venir renforcer le 700 salariés actuels de la société. La société compte sur le télétravail et embaucher dans toute la France ses nouveaux salariés pour faire face à la tension du marché du travail en Ile de France.

Commentaires
Enregistrer un commentaire
🖐 Hello,
N'hésitez pas à commenter ou vous exprimer si vous avez des trucs à dire . . .👉